Wstęp
W tym dziale omówiono i opracowano różne zagadnienia algorytmiczne, jak również struktury danych, których znajomość jest wymagana lub przydatna na maturze.
Przy omawianiu algorytmów często będziemy mówili, że pewne algorytmy są lepsze lub gorsze od innych, ale potrzebujemy do tego jakiejś mierzalnej wielkości, która pozwoli je obiektywnie porównać. Tę wielkość nazywamy w informatyce złożonością (obliczeniową lub pamięciową). Złożoność mówi nam ile z grubsza czasu lub pamięci potrzebuje algorytm do wykonania swojego zadania względem rozmiaru danych wejściowych. Dane wejściowe to nic innego jak argumenty funkcji, czyli na przykład lista, liczba, napis.
A co to oznacza z grubsza? Mamy tu na myśli, że chodzi nam tylko o rząd
wielkości czyli np. 2n to z grubsza n i stała 2 nas nie interesuje.
Podobnie 3n to tyle samo co 2n i n. Jeśli jednak złożoność będzie
wynosiła n^2, to n^2 > n. Łatwiej będzie nam wszystko zrozumieć po
obejrzeniu poniższych przykładów.
Złożoność obliczeniowa
Załóżmy, że nasz algorytm szuka największego elementu na liście. Naturalnym powinno dla nas być, że wystarczy przejrzeć wszystkie elementy listy po kolei i wskazać największy. Możemy to zrobić np. w ten sposób:
def find_max(l: list[int]) -> int:
current_max: int = -1
for e in l:
if e > current_max:
current_max = e
return current_max
Żeby ustalić złożoność obliczeniową tego algorytmu, musimy najpierw ustalić, co
jest rozmiarem danych wejściowych. W tym wypadku będzie to długość listy, którą
oznaczamy jako n. Dla każdego elementu listy musimy wykonać stałą liczbę
operacji - jedno porównanie i ewentualnie jedno przypisanie. W takim razie
dla każdego z grubsza n elementów wykonujemy z grubsza jedną operację.
Złożoność zapisujemy w notacji dużego O, czyli w tym wypadku złożoność to
O(n) (czytamy "o od n").
Złożoność pamięciowa
Złożoność pamięciowa oznacza ile dodatkowej pamięci (poza danymi wejściowymi)
potrzebuje nasz algorytm. Pamięć wejściowa nigdy nie liczy się do złożoności
pamięciowej. Przykładowo funkcja sort() na liście, dostępna w bibliotece
standardowej Pythona, nie wymaga żadnej dodatkowej pamięci, ponieważ sortuje
elementy listy i nie tworzy żadnych nowych list. O takim algorytmie mówimy, że
wymaga pamięci stałej lub działa w miejscu.
Przyjrzyjmy się dwóm poniższym algorytmom, które odwracają elementy pewnej listy:
def list_rev_1(l: list[int]) -> list[int]:
length: int = len(l)
for i in range(length // 2):
tmp: int = l[i]
l[i] = l[length - i - 1]
l[length - i - 1] = tmp
return l
def list_rev_2(l: list[int]) -> list[int]:
res: list[int] = []
for e in l:
res.append(e)
return res
Algorytmy te wyglądają dosyć podobnie, ale pierwszy działa w pamięci stałej,
ponieważ odwraca elementy na liście, którą dostał. Zwróćmy uwagę, że pomimo że
funkcja list_rev_1() zwraca listę, to jest to ta sama lista, co lista wejściowa
i nie wymagała zajęcia żadnej dodatkowej pamięci.
Drugi algorytm działa w pamięci liniowej, ponieważ jeśli długość listy wejściowej
oznaczymy jako n, to musimy stworzyć nową listę o długości n. Zużyliśmy więc
dodatkową pamięć równą O(n) na stworzenie nowej listy tej samej długości.
Złożoność pamięciowa w rekurencji
Należy pamiętać, że każde wywołanie funkcji wymaga stałej pamięci O(1) między
innymi dlatego, że konieczne jest odłożenie wywołania funkcji na stos wywołań.
Jeżeli więc stosujemy algorytmy rekurencyjne, to złożoność pamięciowa będzie
też zależała od liczby wywołań rekurencyjnych.
Poniższa funkcja oblicza n-tą potęgę dwójki przy pomocy rekurencji. Żeby obliczyć
n-tą potęgę musimy wykonać n wywołań rekurencyjnych. Skoro koszt pojedynczego
wywołania to O(1), to złożoność całego algorytmu to O(n).
def pow2(n: int) -> int:
if n < 0:
return -1
if n == 0:
return 1
else:
return 2 * pow2(n - 1)
Nazewnictwo
Więcej przykładów będzie się pojawiało w trakcie poznawania nowych zagadnień algorytmicznych, ale warto zapamiętać kolejność złożoności:
O(1) < O(log(n)) < O(sqrt(n)) < O(n) < O(n*log(n)) < O(n^2)
Różnice widać bardzo wyraźnie na wykresie:
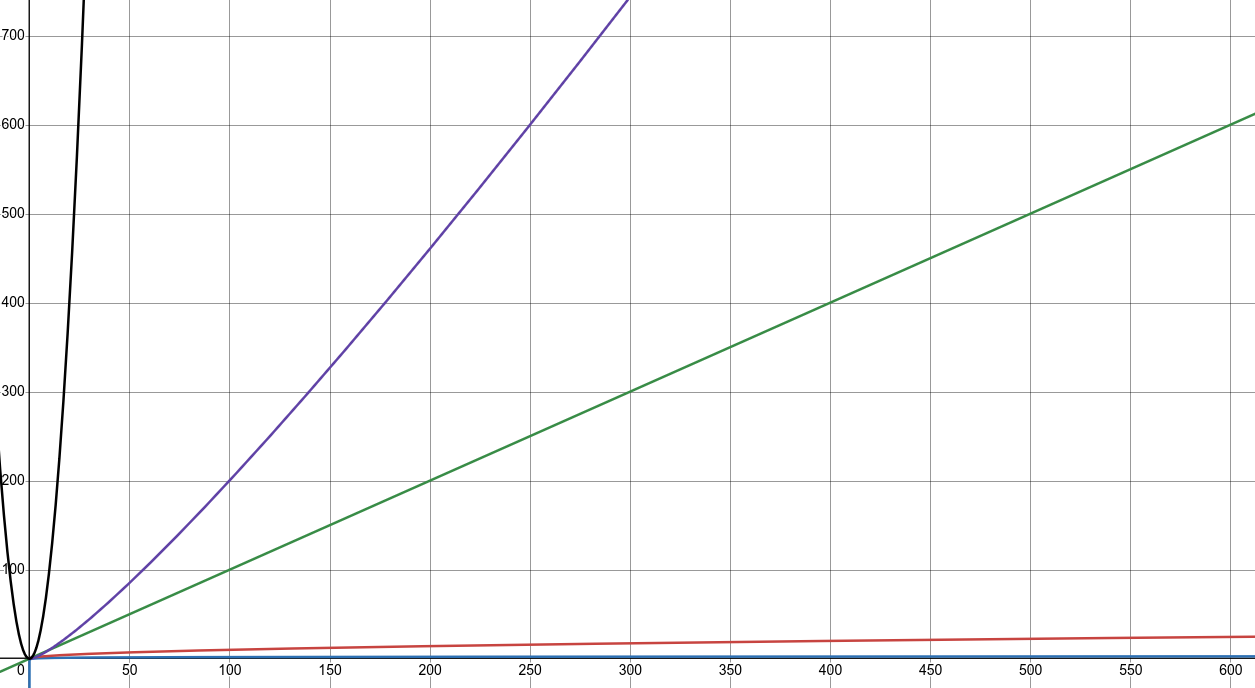
Od wykresu najbliższego osi OX są to:
O(1)- czas/pamięć stała (brak na wykresie)O(log(n))- czas/pamięć logarytmiczna (niebieski)O(sqrt(n))- czas/pamięć pierwiastkowa (czerwony)O(n)- czas/pamięć liniowa (zielony)O(n*log(n))- czas/pamięć liniowo-logarytmiczna (fioletowy)O(n^2)- czas/pamięć kwadratowa (czarny)